Load and Geometry Analyses
Container Lifting Support
- <Container Lifting
- Uniform Loading
- Eccentric Loading
- Tilt and Swing
Contents
C of G for Limiting eccentric payload.
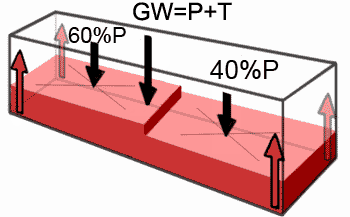 Limiting payload distribution
Limiting payload distribution
1 Position of Centre of Gravity Xc
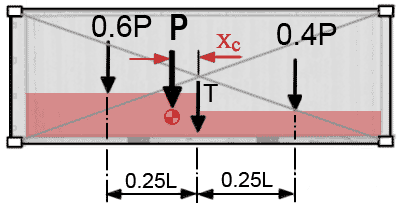 Equivalent point load positions
Equivalent point load positions

2 Level side lifting eccentrically loaded containers.
When bottom side lifting, holding an eccentrically loaded container level can only be achieved using a horizontal top-frame with equal length strops, that may be vertical or angled depending on specific top-frame in use, eg fixed length top-frame Straddle Carriers.
2.1 Vertical corner fitting forces when level lifting.
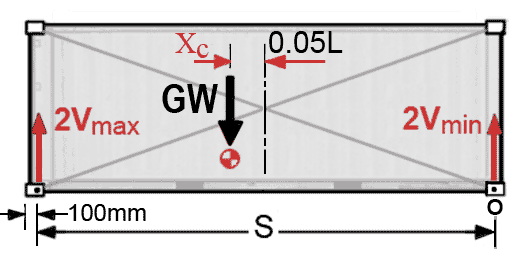 Forces for eccentric loading.
Forces for eccentric loading.
Maximum vertical corner force at the heavy end is:
2.2 Load Factors for Series 1 containers are :
When C of G is central ie, uniformly loaded, Load Factor is 0.25.
3 Sling Forces when level SIDE lifting
 Level lifting forces for offset loading.
Level lifting forces for offset loading.
The sling force F is determined by both its angle α and a proportion of the payload
by the expresion V= F sinα.
The proportion of the GW is expressed in terms of the maximum vertical corner force component V developed above.

4 Vertical corner forces when END lifting.
When end lifting with Side Loaders the lifting arms can be operated independently holding the container level, the following considers this level lifting case. Although longitudinal offset inbalance can be controlled, any transverse eccentricity may result with sideways tilting as C of G re-aligns itself with top lifting point and could be a problem.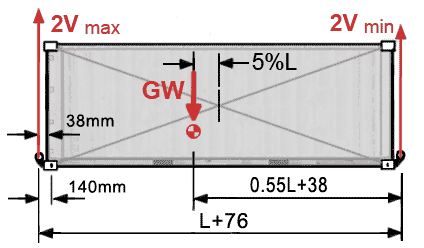 End lifting forces
End lifting forces
The maximum vertical end lifting forces take into account that the end sling forces are further apart, by almost 280mm. When moments are taken about right hand lug load line, the maximum vertical corner force at the 'heavy end' is taken as: Vmax=27.5%Rg
Again the maximum vertical end forces at the heavy end is found from moments about the right hand lug hole centre. The offset load factor never exceeding 0.275 or 27.5%.
4.1 Level lifting Side loader.
 Lifting sling angle α.
Lifting sling angle α.
5 Container Tilt angle induced by offset loading
Lifting is only possible when the C of G is aligned with top lifting point P, and the unit has rotated through the tilt angle θ, shaded in red, for the 3 cases considered, this rotation is evaluated below.
 Positions of C of G's for eccentric loading.
Positions of C of G's for eccentric loading.
Geometry
The geometry, when single point lifting with slings of equal lengths, is shown above with 0.05L longitudinal offset of C of G. Since the height of C of G is the great unknown, vertical positions have been chosen at 25%, 50% and 75% of height H to see what effect it has on the tilt angle.
The tilt angle θ is found from the arctan ratio of x/y ie
The x value is simply the 5%L offset whilst the value of y is distance between C of G and lifting point P ie headroom + position of C of G from the TOP of container. ie
The lug pivots about the position fixed collar 70mm from bottom of corner fitting aperture hence the expression from which the tilt angle is given when C of G is half way up is:

The sling and container assembly rotates about the top lifting point P through the tilt angle θ. The lug pivots about the position fixed collar in the corner fitting aperture, shaded in red for the 3 cases considered, thus eliminating abraision between lug and corner fittings aperture when container is swinging.
When all three C of G positions are considered, resulting tilt angles for 20ft and 40ft units are shown below over sling angle range.
5.1 Container Tilt angle chart for offset C of G
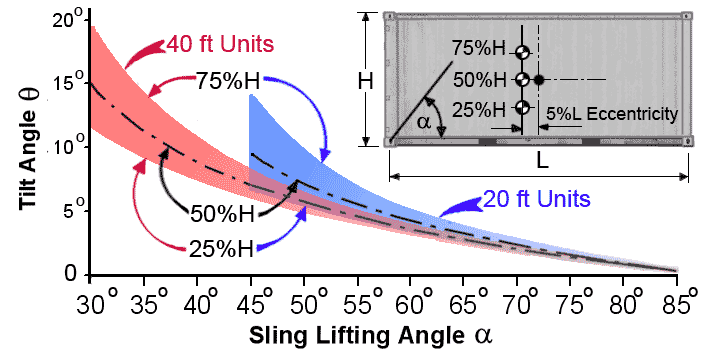 Tilt angles over sling lifting angle range when lifting
Tilt angles over sling lifting angle range when liftingeccentrically loaded 20ft and 40ft containers
these are excessive for short slings and vary with position of C of G, consequently it should always be kept as low as possible.
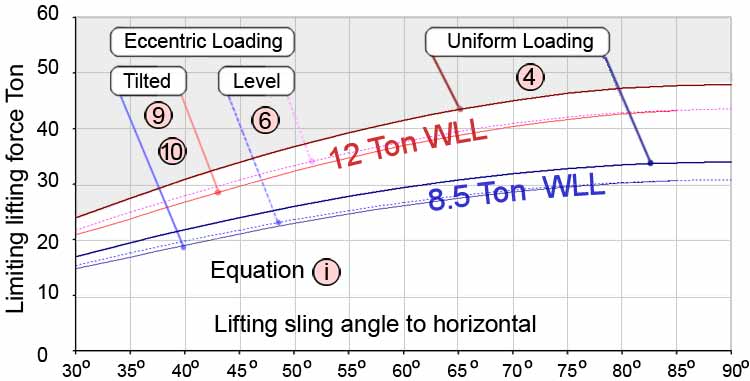
6 Limiting container Gross Weights for eccentric loading.
Lifting via Bottom Lift Sling methods can only take place when C of G is aligned with top lifting point P. The slings of equal length at a specific angle α now includes the tilt angle θ. The GW is formulated to include this angle with slings loaded to WLL of lugs and were found to be approximately 10% lower than those for uniform loading, only the deadload defined in is considered.( Additional live loads may arise when using luffing cranes where load moves in a circular path, eg ship to shore etc, these are transient self equilibriating forces resulting from centripetal force and reactive centrifugal force. Although impractical to quantify such forces, it would be wise to be aware of it's significance when using this lifting mode.)

This arrangement provides a direct method of evaluating limiting gross weights for offset container loading when C of G is aligned with top lifting point. The same three positions of C of G are considered, the highest at 75%H, gives the lowest lifting force for this state. Rather than analyse the corner fitting forces it is simpler to consider the forces at the top lifting point since the sling tension for each leg is constant providing it clears the side of container when spreaders are used. At the lifting point P two slings are connected whilst their bottom ends are attached to lifting lugs and coupled with the side corner fittings. At the 'Heavy End', on the left, the sling force FL cannot exceed the WLL of lugs and, therefore, will dictate the maximum gross weight for combined sling and tilt angles.
The coplaner forces shown at the lifting point mirror those at the corner fittings and for equilibrium the two horizontal forces must be the same for zero motion during a lift. Similarly, the total resolved vertical forces due to total sling tension are limited by WLL of the lugs and these determine the gross weight that can be lifted.
For lifting sling force F, the vertical forces V, and horizontal forces H, are respectively:
From the condition that the horizontal forces are equal, the sling force FR in terms of FL is:
The lifting force Rg is the sum of all the vertical force components hence:
After substituting for FR and simplifying
FL is the maximum tensile force in left hand sling and must not exceed Working Load Limit (WLL) of lug hence substituting FL with WLL gives the limiting gross weight that can be lifted in this case as:
 GW=2WLL[cos(α + θ)tan(α - θ) + sin(α + θ)]
GW=2WLL[cos(α + θ)tan(α - θ) + sin(α + θ)]
7 Alternative Tilt Analysis

This alternative method uses equilibrium of moments about 'O' at the RH corner due to forces acting on the container ie the body force mg or GW, and the resolved H and V components at the LH lug due to sling force F. The magnitude of these forces requires their horizontal distances from point 'O' in terms of lifting sling angle and tilt angle.
In this case the C of G is taken at 0.75 height of 9ft 6in 20ft container for worst case scenario.

8 Limiting Gross Weights for uniform and eccentric container loading.